Graph Structures

PyTensor works by modeling mathematical operations and their outputs using symbolic placeholders, or variables, which inherit from the class Variable. When writing expressions in PyTensor one uses operations like +, -, **, sum(), tanh(). These are represented internally as Ops. An Op represents a computation that is performed on a set of symbolic inputs and produces a set of symbolic outputs. These symbolic input and output Variables carry information about their types, like their data type (e.g. float, int), the number of dimensions, etc.

PyTensor graphs are composed of interconnected Apply, Variable and Op nodes. An Apply node represents the application of an Op to specific Variables. It is important to draw the difference between the definition of a computation represented by an Op and its application to specific inputs, which is represented by the Apply node.

The following illustrates these elements:

Code

import pytensor.tensor as pt

x = pt.dmatrix('x')
y = pt.dmatrix('y')
z = x + y

Diagram

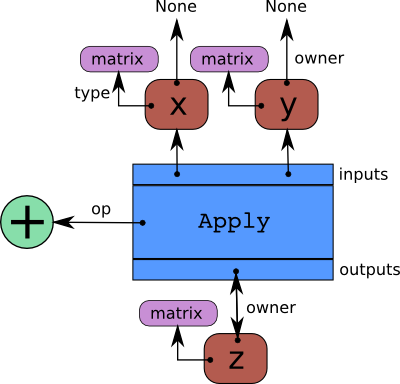
The blue box is an Apply node. Red boxes are Variables. Green circles are Ops. Purple boxes are Types.

When we create Variables and then Apply Ops to them to make more Variables, we build a bi-partite, directed, acyclic graph. Variables point to the Apply nodes representing the function application producing them via their Variable.owner field. These Apply nodes point in turn to their input and output Variables via their Apply.inputs and Apply.outputs fields.

The Variable.owner field of both x and y point to None because they are not the result of another computation. If one of them was the result of another computation, its Variable.owner field would point to another blue box like z does, and so on.

Traversing the graph

The graph can be traversed starting from outputs (the result of some computation) down to its inputs using the owner field. Take for example the following code:

>>> import pytensor
>>> x = pytensor.tensor.dmatrix('x')
>>> y = x * 2.

If you enter type(y.owner) you get <class 'pytensor.graph.basic.Apply'>, which is the Apply node that connects the Op and the inputs to get this output. You can now print the name of the Op that is applied to get y:

>>> y.owner.op.name
'Elemwise{mul,no_inplace}'

Hence, an element-wise multiplication is used to compute y. This multiplication is done between the inputs:

>>> len(y.owner.inputs)
2
>>> y.owner.inputs[0]
x
>>> y.owner.inputs[1]
InplaceDimShuffle{x,x}.0

Note that the second input is not 2 as we would have expected. This is because 2 was first broadcasted to a matrix of same shape as x. This is done by using the OpDimShuffle:

>>> type(y.owner.inputs[1])
<class 'pytensor.tensor.var.TensorVariable'>
>>> type(y.owner.inputs[1].owner)
<class 'pytensor.graph.basic.Apply'>
>>> y.owner.inputs[1].owner.op 
<pytensor.tensor.elemwise.DimShuffle object at 0x106fcaf10>
>>> y.owner.inputs[1].owner.inputs
[TensorConstant{2.0}]

All of the above can be succinctly summarized with the pytensor.dprint() function:

>>> pytensor.dprint(y)
Elemwise{mul,no_inplace} [id A] ''
 |x [id B]
 |InplaceDimShuffle{x,x} [id C] ''
   |TensorConstant{2.0} [id D]

Starting from this graph structure it is easier to understand how automatic differentiation proceeds and how the symbolic relations can be rewritten for performance or stability.

Graph Structures

The following section outlines each type of structure that may be used in an PyTensor-built computation graph.

Apply

An Apply node is a type of internal node used to represent a computation graph in PyTensor. Unlike Variable, Apply nodes are usually not manipulated directly by the end user. They may be accessed via the Variable.owner field.

An Apply node is typically an instance of the Apply class. It represents the application of an Op on one or more inputs, where each input is a Variable. By convention, each Op is responsible for knowing how to build an Apply node from a list of inputs. Therefore, an Apply node may be obtained from an Op and a list of inputs by calling Op.make_node(*inputs).

Comparing with the Python language, an Apply node is PyTensor’s version of a function call whereas an Op is PyTensor’s version of a function definition.

An Apply instance has three important fields:

op

An Op that determines the function/transformation being applied here.

inputs

A list of Variables that represent the arguments of the function.

outputs

A list of Variables that represent the return values of the function.

An Apply instance can be created by calling graph.basic.Apply(op, inputs, outputs).

Op

An Op in PyTensor defines a certain computation on some types of inputs, producing some types of outputs. It is equivalent to a function definition in most programming languages. From a list of input Variables and an Op, you can build an Apply node representing the application of the Op to the inputs.

It is important to understand the distinction between an Op (the definition of a function) and an Apply node (the application of a function). If you were to interpret the Python language using PyTensor’s structures, code going like def f(x): ... would produce an Op for f whereas code like a = f(x) or g(f(4), 5) would produce an Apply node involving the f Op.

Type

A Type in PyTensor provides static information (or constraints) about data objects in a graph. The information provided by Types allows PyTensor to perform rewrites and produce more efficient compiled code.

Every symbolic Variable in an PyTensor graph has an associated Type instance, and Types also serve as a means of constructing Variable instances. In other words, Types and Variables go hand-in-hand.

For example, pytensor.tensor.irow is an instance of a Type and it can be used to construct variables as follows:

>>> from pytensor.tensor import irow
>>> irow()
<TensorType(int32, (1, ?))>

As the string print-out shows, irow specifies the following information about the Variables it constructs:

1. They represent tensors that are backed by numpy.ndarrays. This comes from the fact that irow is an instance of TensorType, which is the base Type for symbolic numpy.ndarrays.

2. They represent arrays of 32-bit integers (i.e. from the int32).

3. They represent arrays with shapes of \(1 \times N\), or, in code, (1, None), where None represents any shape value.

Note that PyTensor Types are not necessarily equivalent to Python types or classes. PyTensor’s TensorType’s, like irow, use numpy.ndarray as the underlying Python type for performing computations and storing data, but numpy.ndarrays model a much wider class of arrays than most TensorTypes. In other words, PyTensor Type’s try to be more specific.

For more information see Types.

Variable

A Variable is the main data structure you work with when using PyTensor. The symbolic inputs that you operate on are Variables and what you get from applying various Ops to these inputs are also Variables. For example, when one inputs

>>> import pytensor
>>> x = pytensor.tensor.ivector()
>>> y = -x

x and y are both Variables. The Type of both x and y is pytensor.tensor.ivector.

Unlike x, y is a Variable produced by a computation (in this case, it is the negation of x). y is the Variable corresponding to the output of the computation, while x is the Variable corresponding to its input. The computation itself is represented by another type of node, an Apply node, and may be accessed through y.owner.

More specifically, a Variable is a basic structure in PyTensor that represents a datum at a certain point in computation. It is typically an instance of the class Variable or one of its subclasses.

A Variable r contains four important fields:

type

a Type defining the kind of value this Variable can hold in computation.

owner

this is either None or an Apply node of which the Variable is an output.

index

the integer such that owner.outputs[index] is r (ignored if Variable.owner is None)

name

a string to use in pretty-printing and debugging.

Variable has an important subclass: Constant.

Constant

A Constant is a Variable with one extra, immutable field: Constant.data. When used in a computation graph as the input of an OpApply, it is assumed that said input will always take the value contained in the Constant’s data field. Furthermore, it is assumed that the Op will not under any circumstances modify the input. This means that a Constant is eligible to participate in numerous rewrites: constant in-lining in C code, constant folding, etc.

Automatic Differentiation

Having the graph structure, computing automatic differentiation is simple. The only thing pytensor.grad() has to do is to traverse the graph from the outputs back towards the inputs through all Apply nodes. For each such Apply node, its Op defines how to compute the gradient of the node’s outputs with respect to its inputs. Note that if an Op does not provide this information, it is assumed that the gradient is not defined.

Using the chain rule, these gradients can be composed in order to obtain the expression of the gradient of the graph’s output with respect to the graph’s inputs.

A following section of this tutorial will examine the topic of differentiation in greater detail.

Rewrites

When compiling an PyTensor graph using pytensor.function(), a graph is necessarily provided. While this graph structure shows how to compute the output from the input, it also offers the possibility to improve the way this computation is carried out. The way rewrites work in PyTensor is by identifying and replacing certain patterns in the graph with other specialized patterns that produce the same results but are either faster or more stable. Rewrites can also detect identical subgraphs and ensure that the same values are not computed twice.

For example, one simple rewrite that PyTensor uses is to replace the pattern \(\frac{xy}{y}\) by \(x\).

See Graph Rewriting and Optimizations for more information.

Example

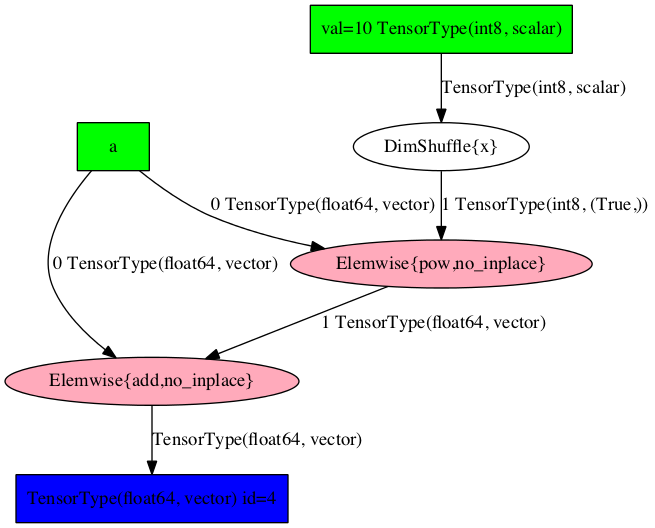
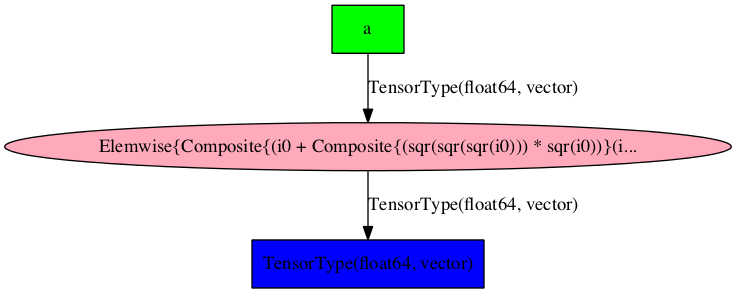
Consider the following example of rewrites:

>>> import pytensor
>>> a = pytensor.tensor.vector("a")      # declare symbolic variable
>>> b = a + a ** 10                    # build symbolic expression
>>> f = pytensor.function([a], b)        # compile function
>>> print(f([0, 1, 2]))                # prints `array([0,2,1026])`
[    0.     2.  1026.]
>>> pytensor.printing.pydotprint(b, outfile="./pics/symbolic_graph_no_rewrite.png", var_with_name_simple=True)  
The output file is available at ./pics/symbolic_graph_no_rewrite.png
>>> pytensor.printing.pydotprint(f, outfile="./pics/symbolic_graph_rewite.png", var_with_name_simple=True)  
The output file is available at ./pics/symbolic_graph_rewrite.png

We used pytensor.printing.pydotprint() to visualize the rewritten graph (right), which is much more compact than the un-rewritten graph (left).

Un-rewritten graph		Rewritten graph