`tensor.fft` – Fast Fourier Transforms#

Performs Fast Fourier Transforms (FFT).

FFT gradients are implemented as the opposite Fourier transform of the output gradients.

Warning

The real and imaginary parts of the Fourier domain arrays are stored as a pair of float arrays, emulating complex. Since pytensor has limited support for complex number operations, care must be taken to manually implement operations such as gradients.

pytensor.tensor.fft.irfft(inp, norm=None, is_odd=False)[source]#

Performs the inverse fast Fourier Transform with real-valued output.

The input is a variable of dimensions (m, …, n//2+1, 2) representing the non-trivial elements of m real-valued Fourier transforms of initial size (…, n). The real and imaginary parts are stored as a pair of float arrays.

The output is a real-valued variable of dimensions (m, …, n) giving the m inverse FFTs.

Parameters:

inp – Array of size (m, …, n//2+1, 2), containing m inputs with n//2+1 non-trivial elements on the last dimension and real and imaginary parts stored as separate real arrays.
norm ({None, 'ortho', 'no_norm'}) – Normalization of transform. Following numpy, default None normalizes only the inverse transform by n, ‘ortho’ yields the unitary transform (\(1/\sqrt n\) forward and inverse). In addition, ‘no_norm’ leaves the transform unnormalized.
is_odd ({True, False}) – Set to True to get a real inverse transform output with an odd last dimension of length (N-1)*2 + 1 for an input last dimension of length N.

pytensor.tensor.fft.rfft(inp, norm=None)[source]#

Performs the fast Fourier transform of a real-valued input.

The input must be a real-valued variable of dimensions (m, …, n). It performs FFTs of size (…, n) on m batches.

The output is a tensor of dimensions (m, …, n//2+1, 2). The second to last dimension of the output contains the n//2+1 non-trivial elements of the real-valued FFTs. The real and imaginary parts are stored as a pair of float arrays.

Parameters:

inp – Array of floats of size (m, …, n), containing m inputs of size (…, n).
norm ({None, 'ortho', 'no_norm'}) – Normalization of transform. Following numpy, default None normalizes only the inverse transform by n, ‘ortho’ yields the unitary transform (\(1/\sqrt n\) forward and inverse). In addition, ‘no_norm’ leaves the transform unnormalized.

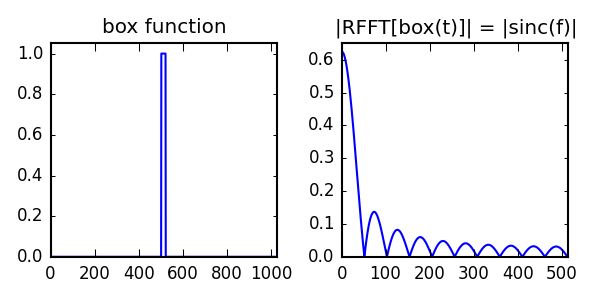
For example, the code below performs the real input FFT of a box function, which is a sinc function. The absolute value is plotted, since the phase oscillates due to the box function being shifted to the middle of the array.

import numpy as np
import pytensor
import pytensor.tensor as pt
from pytensor.tensor import fft

x = pt.matrix('x', dtype='float64')

rfft = fft.rfft(x, norm='ortho')
f_rfft = pytensor.function([x], rfft)

N = 1024
box = np.zeros((1, N), dtype='float64')
box[:, N//2-10: N//2+10] = 1

out = f_rfft(box)
c_out = np.asarray(out[0, :, 0] + 1j*out[0, :, 1])
abs_out = abs(c_out)

tensor.fft – Fast Fourier Transforms#

`tensor.fft` – Fast Fourier Transforms#